Ontologies in Language Model Unembedding Matrices
Authors:- Raymond Ran
(Most of this blog post, experiment design and execution) - Logan Somoza
(Term Frequency calculation; engineering including parallelization of heatmap calculation) - Gabriel Simmons
(wrote TLDR, some editing of this blog post, some guidance on experiments)
- DRAFT; Under construction. Do not cite.
TL;DR:
Park et. al. find that language models represent hierarchical categorical concepts according to a predictable geometric pattern. We investigate how widespread this phenomenon is, how it emerges during training, and its relationship to model size.
1. Background
An ontology is a collection of primitives/concepts that model a certain domain of knowledge (Gruber et al.). Concepts in ontologies are hierarchically connected in parent-child relationships. A parent (also called hypernym) can be thought of as encompassing a child (hyponym). For example, "mammal" is a hypernym to "dog".
1.1 Linear Representation Hypothesis
Park and coauthors consider how LLMs might represent concepts. Since 2013, the field of natural language processing has known that neural networks trained using self-supervision can represent words or concepts as vectors.
Since then, the neural network architectures used for word representation have changed, from single-layer architectures like word2vec to deep architectures based on the Transformer (Vaswani). The typical Transformer LM architecture consists of an embedding matrix, dozens of Transformer blocks, and an output unembedding matrix. Park et. al. are concerned with connecting model behavior (counterfactual word pairs) to concept representations (vectors). The unembedding matrix is the part of the network that translates from vector representation to model output. It’s a natural choice to look at the space spanned by the unembedding matrix.
Park et. al. define the causal inner product - a transformation of a LLM unembedding matrix that preserves language semantics by encoding causally-separable concepts as orthogonal vectors. For Park and coauthors, a concept is defined by a set of counterfactual word pairs, like {(“man”, “woman”), (“king”, “queen”)}. If a language model produces the word “man” as its next output, manipulating the binary gender concept should result in the model producing the output “woman” instead. Two concepts are causally separable if they can be “freely manipulated”. For example, two concepts color (red->blue) and vehicle type (car->truck) are causally separable, since it makes sense to think about a red car, red truck, blue car, or blue truck. But concepts like [...] are not causally separable, since a () () is oxymoronic.
Ontological sets are expansions upon individual concepts, a collection of synonyms of the concept term. These sets are encoded as a vector as a result of retrieving unembeddings of a concept’s synonyms.
Their work confirms the linear representation hypothesis - “that high-level concepts are linearly encoded in the representation spaces of LLMs” (Park 2024). This may already be expected, as we’ve already had examples of word representations that support linear transformations since the 2013 Word2Vec paper. [man woman thing example idk]
Moreover, they show that the concept vectors pointing from child-parent and parent-grandparent nodes in an ontology are orthogonal to each other.
Park et. al.’s theory gives some predictions about what we would expect the model unembedding matrix to look like under the causal inner product. Words belonging to the same concept should have similar vectors, measured using cosine similarity. Words that are ontologically related should have high cosine similarity with each other. Child-parent and parent-grandparent vectors should be orthogonal.
1.2 Linear Representations in Practice
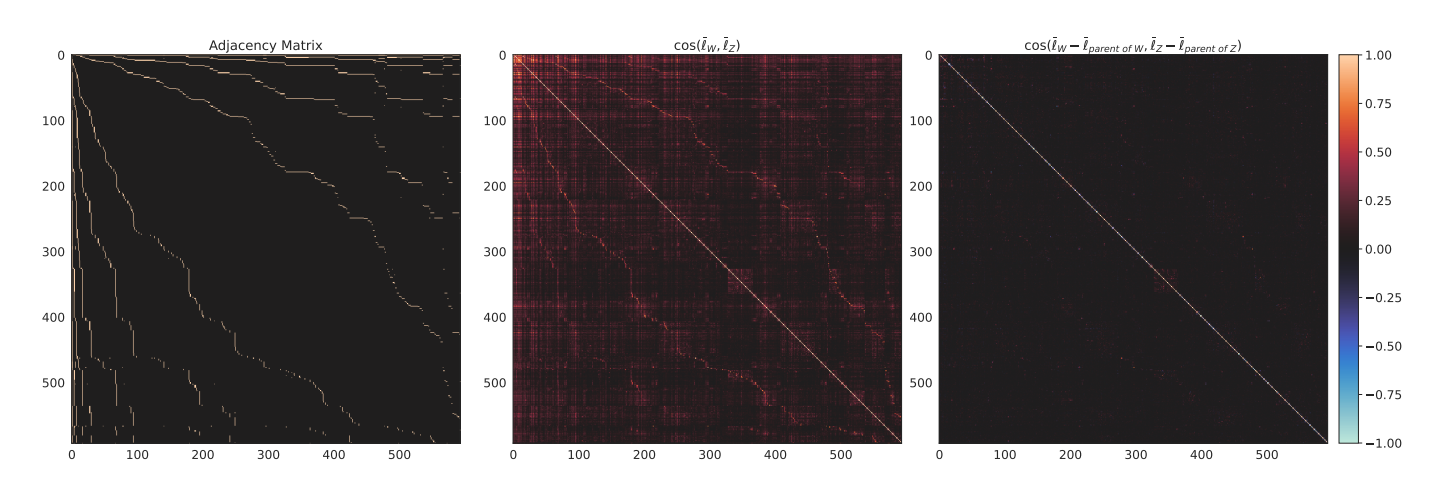
Park et al. shows these relationships with heatmaps, included here as Figure 1. These heatmaps are ordered by concept hierarchy - it would be expected that "entity" be the upper left most entry. The first heatmap is an adjacency matrix describing the child-parent relationship between concepts of an ontology, where a child is adjacent to another concept if descending at any depth. The second heatmap is a cosine similarity matrix between the linear representations of these concepts. As seen in Figure 1, the adjacency matrix is echoed in the second heatmap, suggesting ontological representation in the LLM space. The third heatmap shows cosine similarity between the difference of a concept's and its parent's linear representation. The branches from the adjacency matrix have near-zero values in the third heatmap, demonstrating the orthogonality between the child-parent and parent-grandparent concepts.
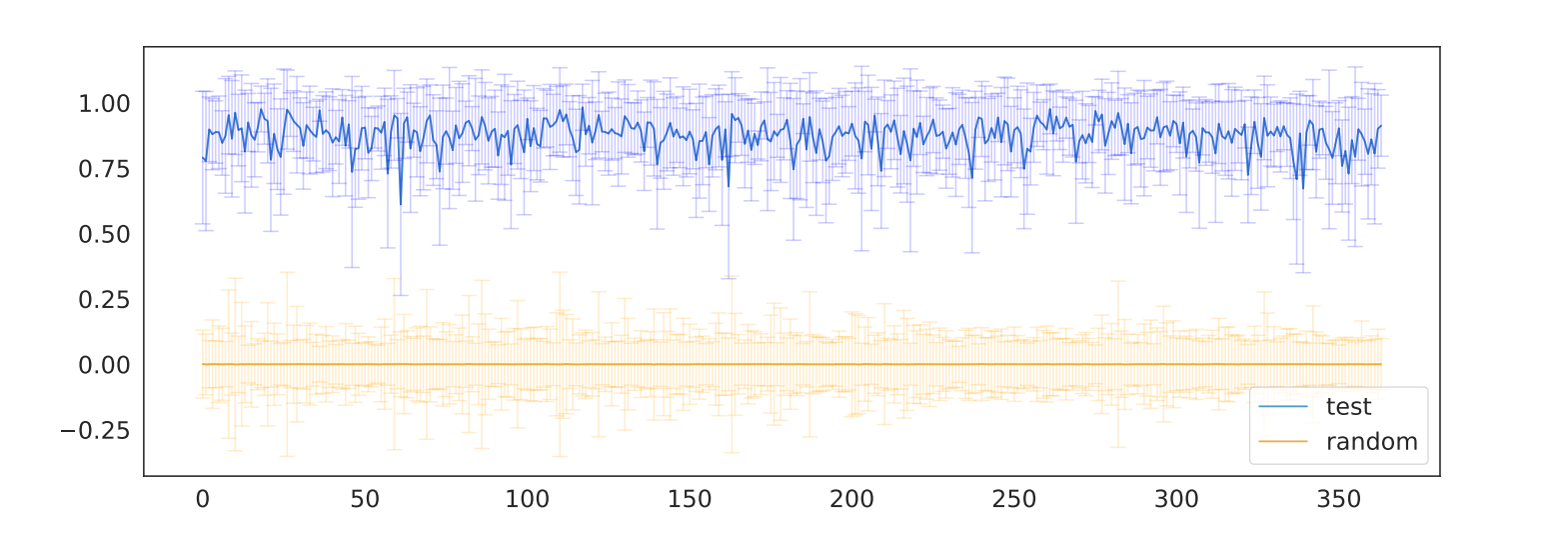
Park et al. also take linear representations of ontological concepts along with random words, and compare the norms of these vectors. As seen in Figure 2, there is a significant gap between the two groups, indicating high level representation of ontological features in the LLM space.
Methods
2.1.1 Evaluating Ontology Representations
Using the formalization from Park et al. as a basis, we introduce three scores for evaluating a model’s ontological maturity.
Linear representation: the average of the concept representation vector norms from Figure 2.
$$ \text{linear-rep-score(model, ontology)} $$ $$ = \mathbb{E}_{\text{binary concepts}}\left(\cos(\text{test-word}, \text{concept vector})\right) $$ $$ \mathbb{E}_{y \in y(w)} \text{proj}(y, \bar{\ell}_w) $$ $$ \text{where } \bar{\ell}_w \text{ is the LDA vector from Park et al.}: $$ $$ \bar{\ell}_w = (\left(\tilde{g}_{w}^{\top}\right)\mathbb{E}(g_{w}))\tilde{g}_{w} $$ $$ \tilde{g}_{w} = \frac{\text{Cov} (g_{w})^\dagger \mathbb{E}(g_{w})}{\left\| \text{Cov} (g_{w})^\dagger \mathbb{E}(g_{w}) \right\|_{2}} $$Causal separability: by comparing the adjacency matrix and cosine similarity of representation vectors from Figure 1, we find the Frobenius norm of the difference between the cosine similarity and adjacency matrices, ignoring the diagonal.
$$ \text{causal-sep-score}(m,o) = \left\| \text{Adj}(o) - \text{off-diag}(\text{cos}(\tilde{\ell}_w), (\tilde{\ell})_z) \right\|_{F} $$Hierarchical: the Frobenius norm of the cosine similarity between child-parent representation differences, disregarding the diagonal as well.
$$ \text{hierarchy-score} = \left\| \mathbb{1} - \text{cos}(\tilde{\ell}_w - \tilde{\ell}_\text{parent of W}, \tilde{\ell}_{Z} - \tilde{\ell}_\text{parent of Z}) \right\|_F $$ $$ \text{where } \mathbb{1} \text{ is the appropriately-sized identity matrix} $$2.1.2 Calculating Representations With Multi-word Lemmas
The heatmaps from Park et al. are generated using single-word lemmas. However, many synsets have lemmas that are multi-word phrases. For example, the synset "entity.n.01" has the lemma "Absolute_space", "Action_plant", etc. To incorporate these multi-word lemmas into the vector representation of the synsets, we take each word of the multi-word lemma and average their unembeddings. [EQUATION HERE]
By including multi-word lemmas, the amount of total lemmas included in the synsets nearly doubles, subsequently allowing more synsets to pass the threshold of lemmas to be included in the heatmaps.
2.1.3 Calcuating Synset-Specific Ontology Scores
In the heatmaps used to calculate causal separability scores, each row corresponds to a synset. For instance, the first row is typically "entity", since synsets were sorted in topological order prior to generating heatmaps.
Using this fact, we propose term ontology scores.
For term linear representation scores, we take the norm of the synset's concept representation vector.
For term causal separability scores, similar to how model causal separability scores are calculated, we take each individual row of the adjacency and cosine similarity heatmaps and find the norm of the difference between the rows (disregarding the diagonal of the cosine similarity heatmap).
For term hierarchy scores, we find the norm of each individual row of the hierarchy heatmap(disregarding the diagonal)
2.1.4 Calculating Term Frequencies
We calculated term frequencies using the Infini-gram python package, an unbounded n-gram model. Infini-gram utilizes a suffix array: a lexicographically sorted integer array containing the starting indices of all suffixes of a corpus. The lexicographically sorted nature of the suffix arrays allows Infini-gram to use binary searches to find and count lexicographically equal occurrences of a given term. Infini-gram achieves \(O(n)\) space and (when searching for a term \(T\)) \(O(logn* |T|)\) searching rather than traditional \(O(n*|T|)\).
2.1.5 Model
For the LLM model, Park et al. uses Google’s Gemma-2b model. However, we use EleutherAI’s Pythia models in our investigation, a collection of models with various parameter sizes with checkpoints in terms of training steps. These include every thousandth step between step1000 and step143000, of which we use the odd thousands (step1000, step3000, …). This allows us to measure the above three scores as a function of training steps.
We use five different sized models: 70M, 160M, 1.4B, 2.8B, and 12B parameters. TODO: [add something about MMLU scores?] Of these, evaluations on 160M, 2.8B, and 12B can be found on the Open LLM Leaderboard. TODO: [link?]
2.1.6 Data
For the ontology, we use the WordNet database as did so by Park et al. in their original exploration. This database contains thousands of synsets (groups of synonyms for a concept), related to one another in a hierarchical fashion. TODO: Describe use of OBO Foundry ontologies
2. Research Question 1: Do longer-trained LLMs have better ontological representations?
Observation 1: Ontological maturity increases with training steps
From each graph, we see a clear improvement in each of the respective scores, an increase in linear representation scores and a decrease in the causal separation and hierarchical scores. This plateaus after sharp improvement, similar to the common trend that models improve mostly at the beginning of training.
Observation 2: Larger models demonstrate improved scores (generally)
The models improve in terms of parameter size as well, where increasingly higher parameter models have better scores with the exception of linear representation, where we see a counter-intuitive pattern, as progressively lower parameter sizes lead to higher scores.
Observation 3: Larger models show more variability in hierarchy and causal separation scores
Looking at the causal separation and hierarchical scores, we see that for 70M and 160M models, scores are relatively smooth throughout training. However, there is more noise in the curves moving down to the larger models. It seems that the noise increases along with model size.
We computed levels of noise by totaling the squared error between the points and a best fit logarithmic function.
This is not the case of linear representation, where all curves are smooth and generally monotonic.
A higher linear representation score means better high-level representation of ontological concepts, as the distinction between these concepts and random words grows.
The decrease in causal separability score is indicative that the reflection of the adjacency matrix is more apparent in the cosine similarity matrix, implying improved representation of ontological categories in the Pythia model space.
The decrease in hierarchical score is indicative of more pronounced orthogonality between child-parent and parent-grandparent pairs, as the cosine similarity between these pairs gets closer and closer to 0.
Research Question 2: How does term depth affect ontology score?
Experiment Setup
We find average depths of synsets in their ontologies. Many synsets have multiple hypernym paths, due to having multiple parents. By averaging the length of all these hypernym paths, we get a depth for each synset.
We generate scatterplots for each ontology, plotting synset depth vs. term causal separability scores. The scores were calculated using heatmaps from Pythia 70M step143000.
Observation 4: Maximum ontology score decreases with term depth
Each synset is colored by their term class. A synset's term class is the highest parent of their hypernym path. Various synsets have multiple hypernym paths, sometimes leading to multiple term classes.
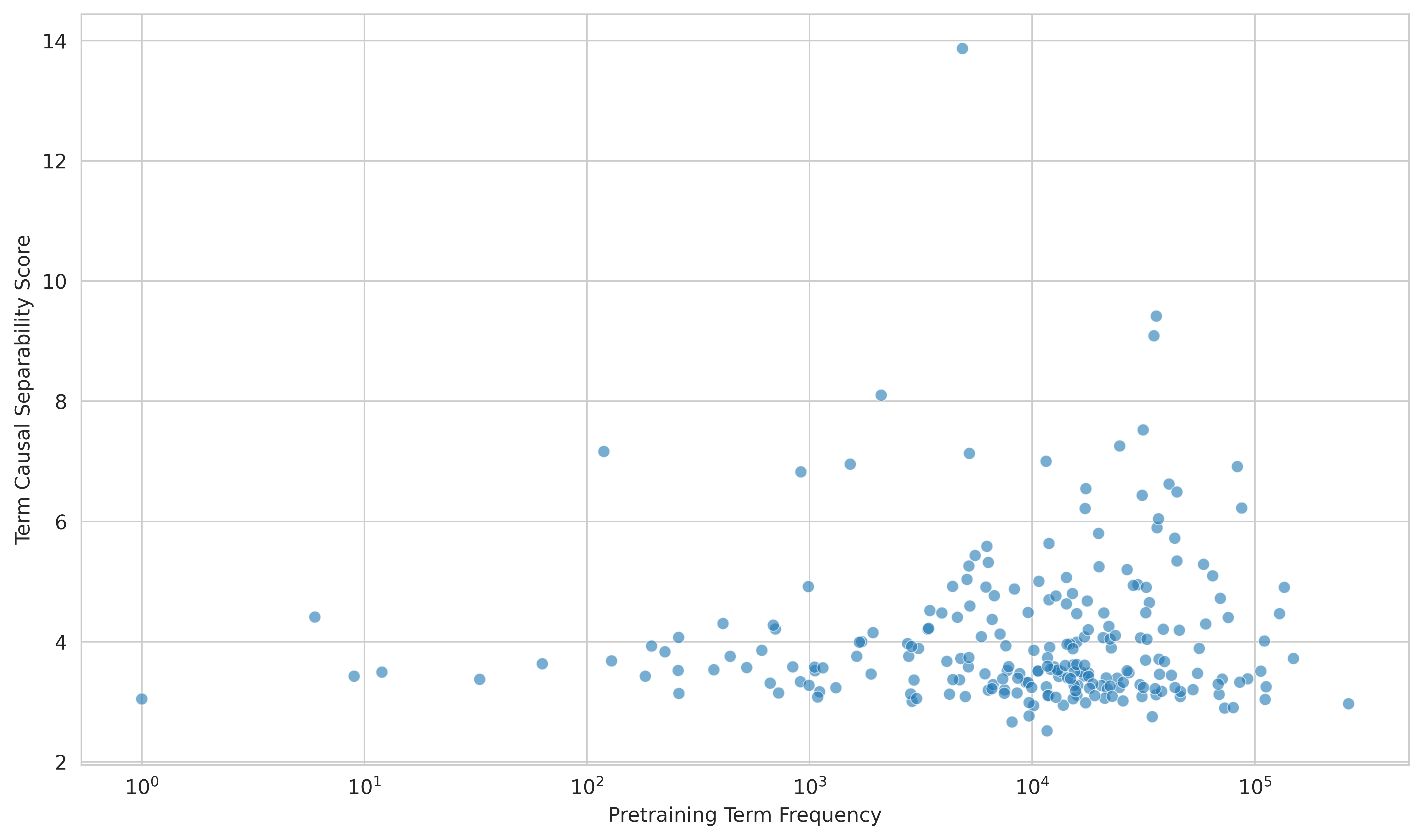
Using Infinigram, we also find corpus pretraining frequencies for each synset name. Pythia models were trained on The Pile dataset. For each term, we find its frequency in The Pile, represented by marker size on the depth scatterplot.
3. Research Question 3: How does term frequency affect ontology score?

4. Research Question 4: Do deeper ontology terms get improved representations later in training?
Alternatively, how does ontology score improvement during training vary by term depth? TODO: Add a figure Line plotApplications
[Content for Applications section]
Future Work
We continue this work with different ontologies, found on OBOFoundry. We also find term frequencies of The Pile, the dataset used to train Pythia models. From this we are able to evaluate a relationship between individual ontology term scores and their respective term frequencies.
